Fonctions et Représentation graphique

I Fonctions

1. Définition

Soit I une partie de l'ensemble des réels (c'est à dire un intervalle ou une réunion d'intervalles de ℝ ),
Définir (ou fabriquer) une fonction sur I, c'est associer à chaque réel x de I, au plus un réel f(x), appelé « image de x »
I est appelé « ensemble de définition » de la fonction.

En d'autres termes :
Une fonction numérique f est une relation entre un ensemble d'objets « initial ou de départ » I et un ensemble d'objets « final ou d'arrivé » J , qui à tout objet x de I associe au plus un objet y de J.

2. Remarques

♢ Le "au plus" de la définition signifie qu'un objet x de l'ensemble de départ I est:

• soit en relation avec un seul objet de l'ensemble d'arrivé J.
• soit en relation avec aucun objet de l'ensemble d'arrivé J
Ces objets peuvent être :

• des points,
• des nombres,
• etc.

♢ Les ensembles de départ et d'arrivé peuvent être :

• le même ensemble d'objets
• des ensembles d'objets différents.

♢ L'image d'un réel x de I par la fonction f est notée f(x) (lire : «f de x »).
Au lieu d'écrire « f est la fonction qui à x associe f(x) », on peut écrire «f :x --> f(x) ».

♢ Lorsque l'ensemble de définition d'une fonction f n'est pas indiqué dans l'énoncé d'un problème, on convient que cet ensemble est l'ensemble de tous les réels pour lesquels on peut calculer f(x).

♢ Une fonction est généralement désignée par l'une des lettres f, g, h ...

3. Exemples et Contre exemple

3.1 Exemples
f(x) = 0,18x + 25
f(x)= -5x + 6
f(x) = 1/x

3.2 Contre exemple
La relation qui à chaque nombre réel positif fait correspondre les deux nombres dont il est le carré, n'est pas une fonction, car au nombre x ne correspond pas un seul nombre.
x = 16 → y₁= -4 ou y₂ = 4
x = 25 → y₁ = -5 ou y₂ = 5
x = 100 → y₁ = -10 ou y₂ = 10

4. Les trois modes de définition d'une fonction

Une fonction peut être définie de trois manières :
• par une formule
• par une courbe
• par un tableau de valeurs.

4.1 Fonction définie par une formule

À un nombre réel, on peut associer :
• son double : x → 2x (tout nombre a un double et un seul) ;
• son carré : x → x² (tout nombre a un carré et un seul).
• .
☺ Fabriquez vous-mêmes deux fonctions définies par une formule !

4.2 Fonction définie par une courbe

• Le graphique suivant est la courbe représentative d'une fonction

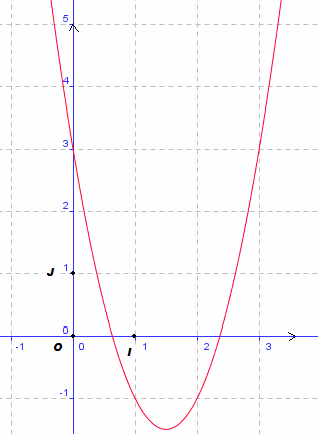
• Le graphique ci-dessous n'est pas la courbe représentative d'une fonction

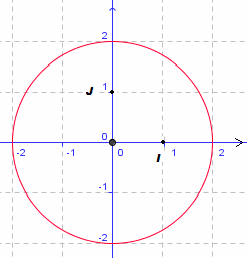
4.3 Fonction définie par un tableau de valeurs

• La longueur ℓ (en cm) d'un ressort en fonction de la masse suspendue m (en kg) est donnée par le tableau de valeurs suivant:

Masse (en kg)	0	1	2	2,5	4	5
longueur (en cm)	10	12	14	15	18	20

• Une fonction affine est définie par le tableau de valeurs ci-dessous :

x	0	2
y= f(x)	4	10

II Représentation graphique

Soit un repère (O; I, J) donné.
Soit f une fonction dont l'ensemble de définition est D_f
La courbe représentative C_f est l'ensemble des points M ayant comme abscisse x et comme ordonnée f(x)
(avec x un réel de l'ensemble de définition D_f )

Exemples
1) Voici une fonction définie par le tableau de valeurs suivant :

x	0	10	15	25	45	60	120
ƒ(x)	25	26,8	27,7	29,5	33,1	35,8	46,6

La courbe représentative de cette fonction est :