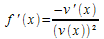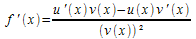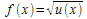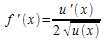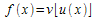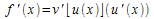Nombre dérivé en a d'une fonction,
Dérivée des fonctions de référence
I Coefficient directeur d'une droite
(Cliquer ici pour plus de détails)
II Tangente à une courbe Cf
Intuitivement, la tangente à une courbe en un point A est une droite qui passe par le point A et qui « effleure » la courbe Cf
III Nombre dérivé en a d'une fonction
1. Définition
|
Soit f : une fonction définie sur un intervalle I Soit Cf : sa courbe représentative dans le plan muni d'un repère Soit a : un nombre réel appartenant à I. On appelle nombre dérivé de f en a, le coefficient directeur de la tangente à Cf au point d'abscisse a On le note f '(a) |

|
2. Nombre dérivé en un réel donné
ActivitéNombre dérivé en un réel donné d'une fonction dont la courbe représentative et la tangente associée sont données
IV Dérivée des fonctions de référence
1. Nombre dérivé en a de la fonction carré x -->x²
ActivitéNombre dérivé en un réel donné de la fonction carré x -->x²
Compléter le tableau ci-dessous
| Abscisse de A : a | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | ... | a |
| Coefficient directeur de la tangente à Cf au point d'abscisse a | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
Conclusion :
On admet que le nombre dérivé en a de la fonction carrée x -->x² est 2a
Et que la fonction dérivée de la fonction carrée f : x -->x² est f ' : x -->2x
2. Nombre dérivé en a de la fonction cube x -->x3
ActivitéNombre dérivé en un réel donné de la fonction cube x -->x3
Compléter le tableau ci-dessous
| Abscisse de A : a | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | ... | a |
| Coefficient directeur de la tangente à Cf au point d'abscisse a | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
Conclusion :
On admet que le nombre dérivé en a de la fonction cube x -->x3 est 3a2
Et que la fonction dérivée de la fonction cube f : x -->x3 est f ' : x -->3x2
3. Nombre dérivé en a de la fonction inverse x -->1/x
ActivitéNombre dérivé en un réel donné de la fonction inverse x -->1/x dans ]0 ; +∞[
Compléter le tableau ci-dessous
| Abscisse de A : a | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | ... | a |
| Coefficient directeur de la tangente à Cf au point d'abscisse a | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
Conclusion :
On admet que le nombre dérivé en a de la fonction inverse x -->1/x est -1/a²
Et que la fonction dérivée de la fonction carrée f : x -->1/x est f ' : x -->-1/x²
4. Nombre dérivé en a de la fonction racine carrée x -->√x
ActivitéNombre dérivé en un réel donné de la fonction racine carrée x -->√x
Compléter le tableau ci-dessous
| Abscisse de A : a | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | ... | a |
| Coefficient directeur de la tangente à Cf au point d'abscisse a | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
Conclusion :
On admet que le nombre dérivé en a de la fonction racine carrée x -->√x est 1/2√a
Et que la fonction dérivée de la fonction racine carrée f : x -->√x est f ' : x -->1/2√x
V Fonction dérivée des fonctions de référence
On admettra les résultats suivants :
| f(x) | f est définie et dérivable sur : | f '(x) |
|---|---|---|
| k (une constante) | ℝ | 0 |
| x | ℝ | 1 |
| x² | ℝ | 2x |
| x3 | ℝ | 3x² |
| xn (si n > 0) | ℝ | nxn-1 |
| 1/x | ℝ * | -1/x² |
| √ x | f est définie sur ℝ+ et f ' est définie sur ℝ +* | 1/(2√x) |
Exercice2
Compléter
La fonction f définie sur ℝ par f(x)=x5, est dérivable sur ℝ et f '(x) = 5x4
La fonction f définie sur ℝ par f(x)=x7, est dérivable sur ℝ et f '(x) = ....
La fonction f définie sur ℝ par f(x)=x11, est dérivable sur ℝ et f '(x) = ..
La fonction f définie sur ℝ par f(x)=3x5 + 6, est dérivable sur ℝ et f '(x) = ...
On considère une fonction f définie sur un intervalle I.
Tous les résultats consignés dans le tableau ci-dessous sont admis.
| u et v sont des fonctions définies et dérivables sur I. Si f(x) s'écrit : | Alors f est dérivable sur I et f '(x) est égale à : | |
|---|---|---|
| Somme | f '(x) = u(x) + v(x) | f '(x) = u'(x) + v'(x) |
| Différence | f(x) = u(x) - v(x) | f '(x) = u'(x) - v'(x) |
| Produit d'une constante par une fonction |
k est une constante et u est une fonction définie sur I
|
|
| Puissance |
n est un entier et u est une fonction définie sur I
|
|
| Inverse |
lorsque v(x) est non nul pour tout x de I
|
|
| Quotient |
lorsque v(x) est non nul pour tout x de I:
|
|
| Racine |
lorsque u(x) est positif pour tout x de I:
f est définie sur R+ et f ' est définie sur ℝ+*
|
|
| Produit de deux fonctions |
u et v sont des fonctions définies et dérivables sur I f(x) = u(x)v(x) |
f'(x) = u'(x)v(x)+ u(x)v'(x) |
| Composé de deux fonctions |
u est définie et dérivable sur I et v définie et dérivable sur J tel que pour tout x de I, u(x) appartient à J
|
|
Remarque
Deux fonctions ayant la même dérivée sur un intervalle diffèrent d'une constante
Exercice3
1) Calculer les fonctions dérivées de chacune des fonctions ci-dessous.
2) Étudier le signe de chacune des fonctions dérivées des fonctions ci-dessous.
a) A(x) = - 5x² sur [-5 ; 5]
b) B(x) = 3x² sur [-3 ; 3]
c) C(x)= -x² + 16x sur [-10 ; 10]
d) D(x) = 2x² + 8x sur [-3 ; 3]
e) E(x)= (x+2)² sur [-5 ; 5]
f) F(x)= -4(x+3)² - 1 sur [-4 ; 4]
g) G(x)= 16(x-3)² - 16 sur [-6 ; 6]
h) H(x)= -5(-x + 1)² + 3 sur [-5 ; 5]
i) K(x) = (2x -5)(8x +5) sur [-4 ; 4]
j)
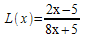
sur [- ∞ ; -5/8[ ⋃ ] -5/8 ; +∞[
Corrigé de l'Exercice3
a) Lorsque k est une constante et que u est une fonction définie sur un intervalle I, nous savons que
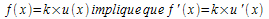
Ici, nous allons poser k = - 5 et u(x) = x² dès lors, u'(x) = 2x et par conséquent:
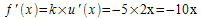
Conclusion :
A(x) = - 5x² implique A'(x) = - 10x
b) B(x) = 3x² implique B'(x) = 6x
c) C(x)= -x² + 16x
Ici, il s'agit de dériver la somme de deux fonctions u définie par u(x) = -x² et v(x) = 16x. Puisque u'(x) = -2x et que v'(x)=16, on peut conclure que C'(x) = -2x + 16
d) D(x) = 2x² + 8x implique D'(x) = 4x + 8
e) E(x)= (x+2)²
Première méthode : utilisation de l'identité remarquable (a+b)² = a²+2ab+b²
E(x)= (x+2)² = x² + 4x + 4
Il suffit ensuite de dériver la somme de trois fonctions u, v et w définies par u(x) = x², v(x) = 4x et w(x) = 4.
On obtient aussitôt :
E'(x) = 2x + 4
Deuxième méthode : utilisation du formulaire :
_html_1fe4490f.gif)
Il suffit de poser n = 2 et de considérer u(x) comme étant x + 2 . On obtient:
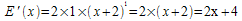
f)
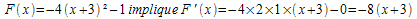
g)
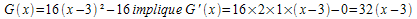
h) H(x)= -5(-x + 1)² + 3 implique H'(x) = (-10)(-1)(-x + 1) + 0 = 10(-x + 1)
i) K(x) = (2x -5)(8x +5)
Ici, il s'agit de dériver le produit de deux fonctions u définie par u(x) = 2x-5 et v définie par v(x) = 8x+5. Puisque u'(x) = 2 et que v'(x)=8, on obtient aussitôt :
K(x) = u(x)v(x) implique K'(x) = u'(x)v(x)+ u(x)v'(x) = 2(8x+5) + (2x - 5)(8) = 16x + 10 + 16x - 40 = 32x -30
j)
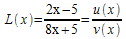
Ici, il s'agit de dériver le quotient de deux fonctions u définie par u(x) = 2x-5 et v définie par v(x) = 8x+5. Puisque u'(x) = 2 et que v'(x) = 8, on obtient aussitôt :
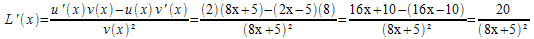
_html_m6c0a29b0.gif)
_html_1269328.gif)
_html_m2294e492.gif)
_html_m2e8fc093.gif)